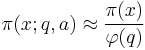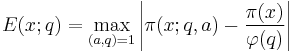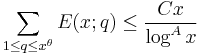Elliott–Halberstam conjecture

In number theory, the Elliott–Halberstam conjecture is a conjecture about the distribution of prime numbers in arithmetic progressions. It has many applications in sieve theory. It is named for Peter D. T. A. Elliott and Heini Halberstam.

To state the conjecture requires some notation. Let 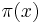\pi(x) denote the number of primes less than or equal to x. If q is a positive integer and a is coprime to q, we let π(x;q,a), denote the number of primes less than or equal to x which are equal to a modulo q. Dirichlet's theorem on primes in arithmetic progressions then tells us that

\pi(x;q,a) \approx \frac{\pi(x)}{\varphi(q)}

when a is coprime to q and \varphi is Euler's totient function. If we then define the error function

E(x;q) = \max_{(a,q) = 1} \left|\pi(x;q,a) - \frac{\pi(x)}{\varphi(q)}\right|

where the max is taken over all a coprime to q, then the Elliott–Halberstam conjecture is the assertion that for every θ < 1 and A > 0 there exists a constant C > 0 such that

\sum_{1 \leq q \leq x^\theta} E(x;q) \leq \frac{C x}{\log^A x}

for all x > 2.

This conjecture was proven for all θ < 1/2 by Enrico Bombieri and A. I. Vinogradov (the Bombieri–Vinogradov theorem, sometimes known simply as "Bombieri's theorem"); this result is already quite useful, being an averaged form of the generalized Riemann hypothesis. It is known that the conjecture fails at the endpoint θ = 1.

The Elliott–Halberstam conjecture has several consequences. One striking one is the recent result announced by Dan Goldston, János Pintz, and Cem Yıldırım,[1] which shows (assuming this conjecture) that there are infinitely many pairs of primes which differ by at most 16.

See also

Notes

  1. ^ arXiv:math.NT/0508185; see also arXiv:math.NT/0505300, arXiv:math.NT/0506067.

References